We (Jeremy and Graham) have a new arXived paper: “The Population Genetic Signature of Polygenic Local Adaptation” (arXived here). This us a cross post from Haldane’s sieve. Comments are welcome there.

The field of population genetics has devoted a lot time to identifying signals of adaptation. These tests are usually predicated on the fact that local adaptation can drive large allele frequency changes between populations. However, we’ve known for almost a century that many traits are highly polygenic, so that adaptation can occur through subtle shifts in allele frequencies at many loci. Until now we’ve been unable to detect such signals, but genome-wide association studies (GWAS) now give us a way of potentially learning about selection on quantitative traits from population genetic data. In this paper we develop a set of approaches to do this in a robust population genetic framework.

GWAS usually assume a simple additive model, i.e. no epistasis/dominance, to test for and estimate effect sizes for a genome-wide set of loci. To test whether local adaptation has shaped the genetic basis of the trait, we do the perhaps boneheaded thing of taking the GWAS results at face value. For each population we simply sum up the product of the frequency at each GWAS SNP and the effect size of that SNP. This gives us an estimate of the mean additive genetic value for the phenotype in each population. This is not the mean phenotype of the population as it ignores the fact that we don’t know all the variants affecting our trait; environmental change across populations, gene by environment interactions, and changes in allele frequencies that have altered the dominance and epistatic relationships between alleles (i.e. all that good stuff that makes life interesting). However, these additive genetic values do have the very useful property that they are simple linear functions of the allele frequencies, which means that we can construct a simple and robust model of genetic drift causing these phenotypes to diverge across populations.

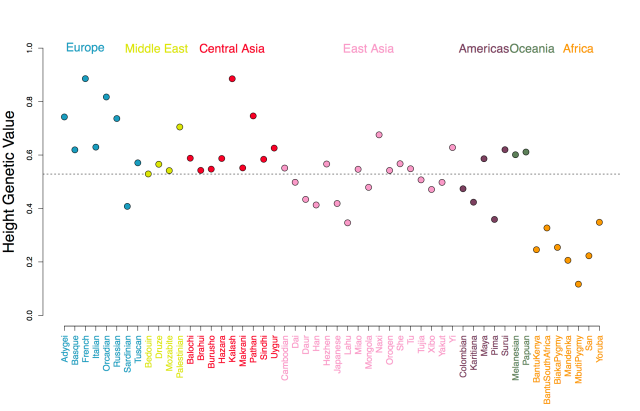
In Figure A we show our estimated genetic values using the human height GWAS of Lango Allen et al (2010). As you can see, populations show deviations around the global mean genetic value, and populations from the same geographic regions covary somewhat in the deviation they take, reflecting the fact that allele frequencies at each GWAS locus tend to covary in their shared genetic drift due to population history and migration. For example in Figure B we show allele frequencies at one of the GWAS height loci.

We can approximately model the allele frequencies at a single locus by assuming that they are multivariate normally distributed around the global mean. The covariance matrix of this distribution is given by a matrix closely related to the kinship matrix of our populations, which can be calculated from a genome-wide sample of putatively neutral loci. As our vector of phenotypic genetic values across populations is simply a weighted sum of the individual allele frequencies, our vector of genetic values is also follows a multivariate Normal distribution. Given that we are summing up lot of loci, even if the multivariate normal model is a poor approximation to drift at one locus, the central limit theorem suggests that it should still be a good fit to the distribution of the genetic values.

This simple neutral model framework, based on multivariate normal distributions, gives us a strong framework to develop tests of selection. Our most basic test is a test for the over-dispersion of the variance of genetic values (i.e. too great an among population variance, once population structure has been accounted for). We also develop a test for an environmental correlations and a way to identify outlier populations and regions to further understand the signal of local adaptation.

We apply our tests to six different GWAS datasets using the HGDP as our set of populations. Our tests reveal wide-spread evidence of selection shaping polygenic traits across populations, although many of the signals are quite subtle. Somewhat surprisingly, we find little evidence for selection on the loci involved in Type 2 diabetes, somewhat of a poster-child for adaptation shaping the genetic basis of a disease thanks to the thrifty gene hypothesis.

We think our approach is a promising way forward to look for selection on the genetic basis of quantitative traits as view by GWAS. However, it also highlights some concerns. In developing our tests we found that we had developed a set of methods that already have equivalents in the quantative trait community– in particular QST, a phenotypic analogy of FST (and its extensions by a number of authors). This raises the question of whether in systems where common garden experiments are possible there is a need to do GWAS if we are only interested in how local adaptation has shaped traits, or if QST style approaches are the best that one can do. We do think that there is much more that could be learnt by our style of approach, but it should also give researchers pause to consider why they want to “find the genes” for local adaptation.

We’ve already gotten some very helpful comments via Haldane’s sieve. We’d love more comments, particularly about points of confusion that could be clarified, other datasets that might be good to apply this to, or other applications we could develop.